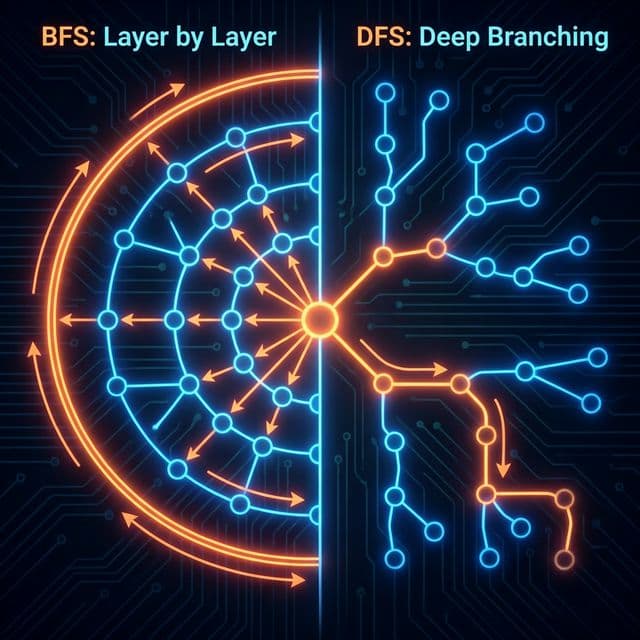
BFS와 DFS: 그래프 탐색의 두 축
미로를 탈출하는 두 가지 방법. 넓게 퍼져나갈 것인가(BFS), 한 우물만 팔 것인가(DFS). 최단 경로는 누가 찾을까?

미로를 탈출하는 두 가지 방법. 넓게 퍼져나갈 것인가(BFS), 한 우물만 팔 것인가(DFS). 최단 경로는 누가 찾을까?
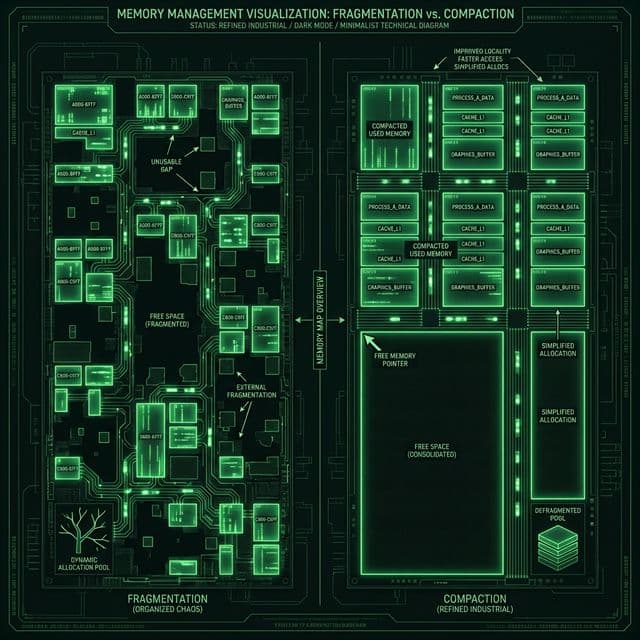
내 서버는 왜 걸핏하면 뻗을까? OS가 한정된 메모리를 쪼개 쓰는 처절한 사투. 단편화(Fragmentation)와의 전쟁.
이름부터 빠릅니다. 피벗(Pivot)을 기준으로 나누고 또 나누는 분할 정복 알고리즘. 왜 최악엔 느린데도 가장 많이 쓰일까요?

매번 3-Way Handshake 하느라 지쳤나요? 한 번 맺은 인연(TCP 연결)을 소중히 유지하는 법. HTTP 최적화의 기본.

DB 설계의 기초. 데이터를 쪼개고 쪼개서 이상 현상(Anomaly)을 방지하는 과정. 제1, 2, 3 정규형을 쉽게 설명합니다.

소셜 네트워크에서 "당신이 알 수도 있는 사람" 기능을 구현해야 하는 상황이었다. "BFS로 풀면 되는 거 아닌가? 근데 왜 큐(Queue)를 써야 하는 거지? DFS로 재귀 돌리면 안 되나?"
그냥 "일단 재귀 돌려서 다 뒤지면 되는 거 아닌가?"라는 생각으로 DFS를 짰고, 결과는 2촌 친구보다 10촌 친구가 먼저 추천되는 엉뚱한 결과. 팀 리드가 조용히 말했다: "가까운 사람부터 추천해야 하는데, DFS로 짜면 최단 거리가 보장이 안 돼요."
그날 나는 이해했다. 문제에 맞는 도구를 쓰지 않으면 안 된다는 것을.
그래프 탐색의 역사는 1736년으로 거슬러 올라간다. 프로이센의 도시 쾨니히스베르크에는 7개의 다리가 있었다. 시민들의 심심풀이 난제는 "이 7개의 다리를 한 번씩만 건너서 원래 자리로 돌아올 수 있는가?"였다.
모두가 발로 뛰어다니며 길을 찾을 때, 레온하르트 오일러(Leonhard Euler)는 방구석에 앉아 지도를 점(Node)과 선(Edge)으로 단순화했다. 이것이 인류 최초의 그래프(Graph)다.
오일러는 "모든 점의 연결선 개수(Degree)가 짝수여야만 돌아올 수 있다"는 것을 증명했고, 쾨니히스베르크의 다리는 홀수점이 있어서 불가능하다는 것을(Impossible) 밝혀냈다. 우리가 지금 배우는 BFS/DFS는 바로 이 오일러의 점과 선을 탐색하는 방법론이다.
실무에서 가장 자주 마주치는 그래프 탐색 알고리즘, BFS(너비 우선 탐색)와 DFS(깊이 우선 탐색)다. 이 둘은 단순히 그래프를 순회하는 방법을 넘어, 문제를 해결하는 두 가지의 철학을 대변한다.
이 글에서는 단순한 암기가 아니라, "도대체 언제 뭘 써야 하는지" 실제 위주로 파헤쳐 본다.
BFS (Breadth-First Search)는 호수에 돌을 던졌을 때 물결이 동심원으로 퍼져나가는 것과 같다. 시작점에서 거리가 1인 곳을 모두 방문하고, 그 다음 거리가 2인 곳을 방문한다.
내가 BFS를 이해한 건 고등학교 과학 시간에 배운 동심원을 떠올렸을 때다. 고요한 호수에 돌을 던지면 물결이 원형으로 퍼져나가는데, 이게 바로 BFS다.
이 방식 덕분에, 어떤 지점에 "처음 도착했다"면 그게 수학적으로 최단 거리라는 것이 보장된다. DFS는 운 좋으면 한 방에 찾지만, 운 나쁘면 지구 한 바퀴를 돌아올 수도 있다.
BFS는 큐(Queue, 선입선출)를 쓴다. "지금 방문한 친구들의 친구들을 줄 서게 해라(Enqueue). 내일 방문할게."
이 줄 서기 시스템 덕분에 순서가 뒤섞이지 않고 층(Level)별 탐색이 가능하다.
처음에는 "왜 큐를 쓰는 거지?"라는 의문이 들었는데, 결국 이거였다. "먼저 발견한 놈을 먼저 처리하면, 가까운 놈부터 처리된다"는 단순한 진리.
DFS (Depth-First Search)는 미로를 푸는 사람의 행동과 똑같다. "오른쪽 벽에 손을 대고 막다른 길이 나올 때까지 계속 걷는다."
어렸을 때 미로 찾기 책에서 배운 꼼수가 있다. "오른손을 벽에 대고 계속 걷기". 막다른 길이 나와도 괜찮다. 다시 돌아오면서 왼쪽 길을 시도하면 된다. 이게 바로 DFS의 본질이다.
내가 이 개념을 받아들인 건, 실제로 명동 골목길에서 길을 잃었을 때였다. "일단 이 골목 끝까지 가보자. 아니면 돌아오면 되지." 이게 DFS다.
DFS는 스택(Stack, 후입선출)을 쓰거나, 재귀 함수를 쓴다. 재귀 함수가 호출될 때마다 시스템 스택(Call Stack)에 층층이 쌓이기 때문이다. 구현 코드가 BFS보다 훨씬 짧고 간결해서, 알고리즘 문제에서 "그냥 다 뒤져봐야 하는 문제"가 나오면 일단 DFS부터 짜는 게 국룰이다.
하지만 여기에 큰 함정이 있다.
DFS의 치명적인 단점은 깊이가 너무 깊어지면 터진다는 것이다. 노드 1개가 재귀 1번이라고 치면, 노드가 10만 개가 일직선으로 연결되어 있을 때 재귀도 10만 번 일어난다. 보통 언어들의 기본 재귀 한계치는 1,000 ~ 10,000 정도다.
내가 처음 백준에서 DFS 문제를 풀다가 RecursionError를 만났을 때의 당황스러움이 아직도 생생하다. "내 코드 논리는 맞는데, 왜 터지는 거야?"
해결책은 재귀 대신 명시적인 스택(Explicit Stack)을 사용해서 힙(Heap) 메모리를 쓰도록 구현하는 것이다. 힙은 스택보다 훨씬 크니까 안전하다.
DFS를 구현할 때 보통 재귀로 짠다. 하지만 그래프가 매우 깊으면 "Stack Overflow가 발생하면 어떻게 할까?"라는 문제가 생긴다. 그때는 명시적인 스택(Explicit Stack)을 써서 반복문으로 짜야 한다.
def dfs_recursive(node, visited):
visited.add(node)
for neighbor in graph[node]:
if neighbor not in visited:
dfs_recursive(neighbor, visited)
def dfs_iterative(start_node):
stack = [start_node]
visited = set()
while stack:
node = stack.pop() # 스택에서 꺼냄 (LIFO)
if node not in visited:
visited.add(node)
# 스택의 특성상 나중에 넣은 게 먼저 나옴 -> 순서 뒤집힘 주의
stack.extend(reversed(graph[node]))
BFS/DFS가 가장 빛을 발하는 문제는 "연결된 덩어리(Connected Component) 찾기"다. 지도상에 '1'(땅)과 '0'(바다)이 있을 때, 섬이 몇 개인지 세는 문제(LeetCode 200번)가 교과서다.
def numIslands(grid):
if not grid: return 0
count = 0
rows, cols = len(grid), len(grid[0])
def dfs(r, c):
# 범위를 벗어나거나, 물(0)이거나, 이미 방문했으면(2) 종료
if r < 0 or c < 0 or r >= rows or c >= cols or grid[r][c] != '1':
return
grid[r][c] = '0' # 방문 처리 (땅을 가라앉힘)
# 동서남북 탐색
dfs(r+1, c)
dfs(r-1, c)
dfs(r, c+1)
dfs(r, c-1)
for r in range(rows):
for c in range(cols):
if grid[r][c] == '1': # 새로운 땅 발견!
count += 1
dfs(r, c) # 연결된 모든 땅을 가라앉힘
return count
이중 for문을 돌다가 땅('1')을 만나면 count를 1 올리고, dfs를 발동시켜서 그 땅과 연결된 모든 땅을 '0'으로 지워버린다.
예를 들어 이런 지도가 있다고 생각해보자.
1 1 0 0
1 0 0 1
0 0 1 1
count = 1count = 2count = 3결과: 섬 3개.
직관적이고 강력하다. 처음 이 코드를 이해했을 때, "아, 이게 그래프 탐색의 진짜 힘이구나"라고 와닿았다.
백준 "숨바꼭질" 문제를 풀 때였다. 수빈이가 동생을 찾는 최단 시간을 구하는 문제였는데, 나는 습관적으로 DFS를 짰다. "일단 끝까지 가보고 최솟값 갱신하면 되겠지."
결과는 시간 초과.
왜냐하면 DFS는 최단 경로를 보장하지 않기 때문에, 모든 경로를 다 탐색해봐야 한다. 경우의 수가 수만 가지인데, 다 뒤지려니 시간이 터진 것이다.
BFS로 다시 짰더니 0.1초 만에 통과. BFS는 "처음 도착한 순간 = 최단 거리"이기 때문에, 도착하는 즉시 답을 반환하면 끝이다.
이때 정리해본 교훈:
서울에서 부산까지 최단 경로를 찾을 때, 서울에서만 출발하는 게(BFS) 아니라, 서울과 부산 양쪽에서 동시에 출발하면 어떨까? 두 원이 중간에서 만나는 순간 탐색이 종료된다. 탐색 범위가 기하급수적으로 줄어드는 엄청난 최적화 기법이다.
내가 이 개념을 받아들인 건, "아, 이거 경찰이 도둑 잡을 때 쓰는 방법이잖아?"라고 생각했을 때다. 경찰은 범죄 현장에서, 도둑의 집에서 동시에 수사를 시작한다. 어디선가 만나면 범인 체포.
BFS는 메모리를 너무 많이 먹고(큐가 폭발), DFS는 최단 경로 보장이 안 된다. 이 둘의 장점만 합친 혼종이 있다.
"처음부터 다시 하면 손해 아닌가요?" 싶지만, 트리의 특성상 하위 노드가 압도적으로 많기 때문에 상위 노드 몇 번 다시 방문하는 건 비용도 아니다. 인공지능(체스 엔진)에서 매우 애용하는 방식이다.
BFS는 "모든 간선의 거리가 1일 때"만 최단 경로를 보장한다. 만약 어떤 길은 1km, 어떤 길은 10km라면? BFS는 거리를 무시하고 "단계(Hop)"만 따지기 때문에 틀린 답을 내놓는다.
이때 필요한 것이 다익스트라 알고리즘이다. 다익스트라는 사실 업그레이드된 BFS다.
import heapq
def dijkstra(start):
pq = [(0, start)] # (거리, 노드)
distances = {node: float('inf') for node in graph}
distances[start] = 0
while pq:
curr_dist, curr_node = heapq.heappop(pq) # 가장 가까운 노드 꺼냄
if curr_dist > distances[curr_node]:
continue
for neighbor, weight in graph[curr_node].items():
cost = curr_dist + weight
if cost < distances[neighbor]: # 더 빠른 길 발견!
distances[neighbor] = cost
heapq.heappush(pq, (cost, neighbor))
"큐를 우선순위 큐로 바꾼다"는 점만 빼면 BFS와 구조가 똑같다.
| 상황 | 추천 알고리즘 | 이유 |
|---|---|---|
| 최단 거리를 찾아라 | BFS | 가까운 곳부터 훑으니까 무조건 정답. |
| 경로의 특징을 저장해야 함 | DFS | 경로 그 자체를 스택에 저장하니까. |
| 그래프가 진짜 큼 | DFS | BFS는 큐에 다 담다가 메모리 터짐. |
| 깊이가 무한대일 수도 있음 | BFS | DFS는 영원히 돌아오지 못할 수도 있음. |
| 가중치가 있는 그래프 | Dijkstra | BFS는 가중치를 무시함. |
"망치(DFS)를 든 사람에게는 모든 못(그래프)이 박아야 할 대상으로 보인다"는 말이 있다. 하지만 우리는 드라이버(BFS)도 가지고 있어야 한다. 문제의 특성(최단 경로냐, 완주냐)을 보고 도구를 골라 잡는 것이 엔지니어의 실력이다.
내가 이 두 알고리즘을 제대로 이해한 건, "언제 뭘 써야 하는지"를 몸으로 부딪히면서 깨달았을 때였다. 이론은 금방 잊어버리지만, 실수는 오래 남는다.
Imagine you have lost your keys in your house. How do you search?
This is the fundamental difference between Breadth-First Search (BFS) and Depth-First Search (DFS).
BFS explores neighbors first, then neighbors of neighbors. It radiates out from the start node like a ripple in a pond.
BFS uses a Queue (First-In, First-Out).
If all edges have the same weight (e.g., distance is always 1), BFS is guaranteed to find the shortest path. Why? Because it checks everything at Distance 1, then Distance 2... So the first time it sees the target, that is mathematically the shortest route.
Usage:
DFS picks one path and follows it until the bitter end. If it hits a wall, it retraces its steps (Backtracks) to the last intersection and tries the next path.
DFS uses a Stack (Last-In, First-Out).
function calls itself) naturally behaves like a stack.DFS is often more memory friendly than BFS.
Usage:
Let's implement both for a simple graph.
function bfs(startNode) {
const queue = [startNode];
const visited = new Set([startNode]);
while (queue.length > 0) {
const node = queue.shift(); // Remove from FRONT (Queue)
console.log(node);
for (const neighbor of graph[node]) {
if (!visited.has(neighbor)) {
visited.add(neighbor);
queue.push(neighbor); // Add to BACK
}
}
}
}
function dfs(node, visited = new Set()) {
console.log(node);
visited.add(node);
for (const neighbor of graph[node]) {
if (!visited.has(neighbor)) {
dfs(neighbor, visited); // Recursion (Stack)
}
}
}
Change queue.shift() to stack.pop() in the iterative version, and BFS becomes DFS.
The structure is identical; only the container (Queue vs Stack) changes.
BFS and DFS are just the grandfathers. Modern algorithms are their children.
BFS assumes all edges have weight 1. What if roads have different lengths? (Traffic, Highway vs Local). Dijkstra is BFS, but instead of a simple Queue, it uses a Priority Queue.
Queue.pop()PriorityQueue.pop_min()DFS is memory efficient but might go down an infinite hole. BFS is optimal but explodes memory. IDDFS combines both.
Used for Build Systems (Webpack, Make) or Package Managers (npm). "Library A depends on B. B depends on C." Order: C -> B -> A. How to find this?
BFS is great, but if the graph is huge, the "wave" gets too big (exponential growth). Optimization: Start BFS from the Start Node AND the Target Node simultaneously. When the two waves meet in the middle, you found the path. This drastically reduces the search space (Area of two small circles < Area of one big circle).
How to detect infinite loops? We need 3 states: 0. White: Unvisited.
If you meet a Gray node, it's a Cycle!
function hasCycle(graph) {
const visited = new Map(); // 0, 1, 2
function dfs(node) {
if (visited.get(node) === 1) return true; // Cycle!
if (visited.get(node) === 2) return false; // Already safe
visited.set(node, 1); // Mark Gray
for (let neighbor of graph[node]) {
if (dfs(neighbor)) return true;
}
visited.set(node, 2); // Mark Black
return false;
}
for (let node in graph) {
if (dfs(node)) return true;
}
return false;
}
DFS is not just for solving methods. It CREATES mazes.
This creates "Perfect Mazes" (One unique path between any two points).
A: Yes.
If the graph is very deep (e.g., a linked list of length 100,000), the recursion stack will blow up.
(JavaScript/Python usually limit recursion to ~10,000 frames).
Solution: Use an Iterative DFS with an explicit Stack [] in Heap memory. Heap is much larger than Call Stack.
A: Dijkstra handles Weighted Edges. BFS treats all edges as "Cost 1". If you are building a Map App:
A: It's a hybrid trick.
You want Shortest Path (BFS benefit) but low memory (DFS benefit).
You run DFS with depth_limit=1. If not found, run with depth_limit=2.
It feels like wasted CPU work, but because the leaves of a tree outnumber the inner nodes, re-visiting top nodes is cheap.
It is the standard algorithm for AI Game Solvers (Chess engines).
A: A* is Dijkstra + Heuristic. Dijkstra scans in a circle (blindly). A* scans towards the target (using a hint like "Target is North"). It is the gold standard for games and maps.
Graph Theory (the mother of BFS/DFS) started with a puzzle. In 1736, the city of Konigsberg (Prussia) had 7 bridges. The people asked: "Can we walk through all 7 bridges exactly once and return home?"
Leonhard Euler proved it was impossible. He didn't walk the bridges. He drew dots (nodes) and lines (edges). He realized that to enter and leave a node, you need an even number of bridges (Degree). This abstraction (Nodes + Edges) gave birth to Graph Theory. Without Euler, we wouldn't have BFS, DFS, or the Internet today.