
퀵 정렬(Quick Sort): 분할 정복의 대표
이름부터 빠릅니다. 피벗(Pivot)을 기준으로 나누고 또 나누는 분할 정복 알고리즘. 왜 최악엔 느린데도 가장 많이 쓰일까요?

이름부터 빠릅니다. 피벗(Pivot)을 기준으로 나누고 또 나누는 분할 정복 알고리즘. 왜 최악엔 느린데도 가장 많이 쓰일까요?
내 서버는 왜 걸핏하면 뻗을까? OS가 한정된 메모리를 쪼개 쓰는 처절한 사투. 단편화(Fragmentation)와의 전쟁.
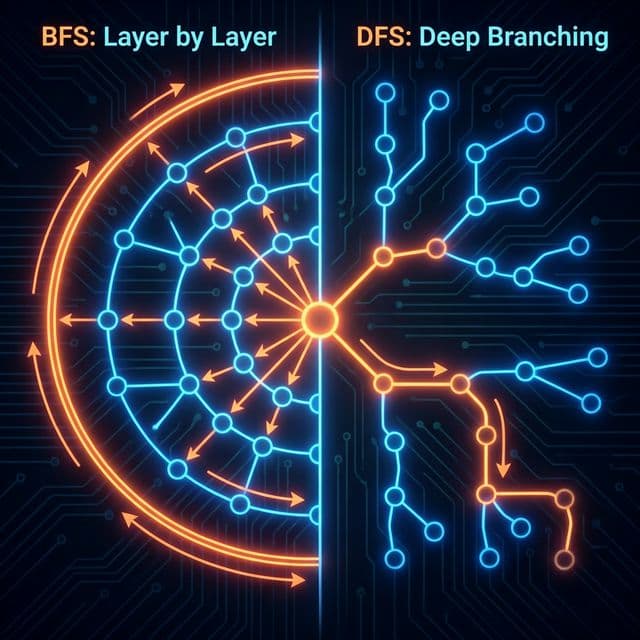
미로를 탈출하는 두 가지 방법. 넓게 퍼져나갈 것인가(BFS), 한 우물만 팔 것인가(DFS). 최단 경로는 누가 찾을까?
매번 3-Way Handshake 하느라 지쳤나요? 한 번 맺은 인연(TCP 연결)을 소중히 유지하는 법. HTTP 최적화의 기본.

DB 설계의 기초. 데이터를 쪼개고 쪼개서 이상 현상(Anomaly)을 방지하는 과정. 제1, 2, 3 정규형을 쉽게 설명합니다.

알고리즘 공부할 때 정렬 알고리즘 공부하면서 버블 정렬, 선택 정렬, 삽입 정렬까지는 그럭저럭 따라갔다. 느리긴 해도 직관적이었다. 그런데 퀵 정렬(Quick Sort)을 처음 봤을 땐 머리가 복잡했다. "이름은 Quick인데 왜 최악의 경우엔 O(N²)야?", "그럼 왜 실제로 가장 많이 쓰인다는 거지?", "Pivot을 어떻게 골라야 빠른 거야?" 같은 질문이 꼬리를 물었다.
책에선 재귀 코드가 짧게 나와 있었지만, 실제로 어떻게 돌아가는지, 왜 병합 정렬보다 메모리를 덜 쓰는지, Lomuto 방식이랑 Hoare 방식은 뭐가 다른지, 3-way partition은 또 무엇인지 감이 안 잡혔다. 그저 "Pivot을 기준으로 작은 건 왼쪽, 큰 건 오른쪽으로 보낸다"는 말만 반복해서 읽었던 기억이 난다.
퀵 정렬을 이해하려고 직접 배열을 손으로 쪼개보기 시작했다.
[7, 3, 9, 1, 5]
Pivot을 5로 잡으면,
이렇게 분할된다. 그다음 왼쪽 [3, 1]에서 Pivot을 1로 잡으면 [1, 3]으로 정렬되고, 오른쪽 [7, 9]에서 Pivot을 7로 잡으면 [7, 9]로 정렬된다. 합치면 [1, 3, 5, 7, 9]가 된다.
핵심은 Pivot을 어떻게 골라서 어떻게 배열을 나누는지였다. Pivot을 잘못 고르면—예를 들어 이미 정렬된 배열 [1, 2, 3, 4, 5]에서 맨 끝 요소를 계속 Pivot으로 잡으면—한쪽은 텅 비고 한쪽엔 N-1개가 남아 트리가 일직선이 되어 O(N²)이 된다는 걸 깨달았다.
이게 재귀 트리(Recursion Tree) 분석의 핵심이었다. 균형 잡힌 분할이 일어나면 트리 깊이가 log N이 되어 각 레벨에서 O(N)씩 처리하니 총 O(N log N)이 나온다. 하지만 한쪽으로 치우치면 트리 깊이가 N이 되어 O(N²)이 나온다.
퀵 정렬의 핵심은 Partition 연산이다. 배열을 Pivot 기준으로 두 부분으로 나누는 과정인데, 대표적으로 두 가지 방식이 있다.
Lomuto 방식은 이해하기 쉽다. Pivot을 배열 끝으로 잡고, 왼쪽부터 순회하면서 Pivot보다 작은 원소를 앞쪽으로 모은다.
function lomutoPartition(arr, low, high) {
const pivot = arr[high]; // 맨 끝을 Pivot으로 선택
let i = low - 1; // 작은 원소들의 경계선
for (let j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
[arr[i], arr[j]] = [arr[j], arr[i]]; // swap
}
}
[arr[i + 1], arr[high]] = [arr[high], arr[i + 1]]; // Pivot을 중간에 배치
return i + 1; // Pivot의 최종 위치
}
장점: 코드가 직관적이다. 단점: Swap 횟수가 많고, 이미 정렬된 배열에서 비효율적이다.
Hoare 방식은 Tony Hoare(퀵 정렬 창시자)가 만든 원조 방식이다. 양쪽 끝에서 포인터를 좁혀가며 Pivot보다 큰 것과 작은 것을 교환한다.
function hoarePartition(arr, low, high) {
const pivot = arr[low]; // 맨 앞을 Pivot으로 선택
let i = low - 1;
let j = high + 1;
while (true) {
do { i++; } while (arr[i] < pivot);
do { j--; } while (arr[j] > pivot);
if (i >= j) return j; // 포인터가 교차하면 종료
[arr[i], arr[j]] = [arr[j], arr[i]]; // swap
}
}
장점: Swap 횟수가 적고 평균적으로 빠르다. 단점: 코드가 약간 복잡하고, Pivot의 최종 위치가 명확하지 않을 수 있다.
실제로는 Lomuto가 구현 단순함 덕에 많이 쓰이지만, 성능이 중요한 라이브러리(예: C++ std::sort)는 Hoare 방식이나 변형을 쓴다.
Pivot을 어떻게 고르느냐에 따라 퀵 정렬의 성능이 극적으로 달라진다.
가장 단순한 방법. 배열이 이미 정렬되어 있거나 역정렬되어 있으면 최악의 경우 O(N²)이 발생한다.
배열에서 무작위로 원소를 골라 Pivot으로 쓴다. 최악의 경우를 확률적으로 회피한다. 실제로 많이 쓰인다.
function randomPivot(arr, low, high) {
const randomIndex = low + Math.floor(Math.random() * (high - low + 1));
[arr[randomIndex], arr[high]] = [arr[high], arr[randomIndex]];
return lomutoPartition(arr, low, high);
}
배열의 첫 번째, 중간, 마지막 원소 중 중간값을 Pivot으로 선택한다. 극단적인 값이 Pivot이 되는 것을 방지한다.
function medianOfThree(arr, low, high) {
const mid = Math.floor((low + high) / 2);
if (arr[low] > arr[mid]) [arr[low], arr[mid]] = [arr[mid], arr[low]];
if (arr[low] > arr[high]) [arr[low], arr[high]] = [arr[high], arr[low]];
if (arr[mid] > arr[high]) [arr[mid], arr[high]] = [arr[high], arr[mid]];
[arr[mid], arr[high]] = [arr[high], arr[mid]]; // 중간값을 끝으로
return lomutoPartition(arr, low, high);
}
Pivot과 같은 값이 많은 배열(예: [5, 3, 5, 5, 1, 5, 9])에서는 2-way partition이 비효율적이다. 같은 값을 계속 재귀로 처리하게 되기 때문이다.
3-Way Partition은 배열을 세 구간으로 나눈다:
function quickSort3Way(arr, low, high) {
if (low >= high) return;
let lt = low; // Pivot보다 작은 구간의 끝
let gt = high; // Pivot보다 큰 구간의 시작
let i = low;
const pivot = arr[low];
while (i <= gt) {
if (arr[i] < pivot) {
[arr[lt], arr[i]] = [arr[i], arr[lt]];
lt++;
i++;
} else if (arr[i] > pivot) {
[arr[i], arr[gt]] = [arr[gt], arr[i]];
gt--;
} else {
i++; // Pivot과 같으면 그냥 넘어감
}
}
quickSort3Way(arr, low, lt - 1); // 작은 구간 재귀
quickSort3Way(arr, gt + 1, high); // 큰 구간 재귀
// 같은 구간(lt ~ gt)은 이미 정렬 완료
}
중복이 많은 데이터에서 3-Way Partition은 성능 개선이 크다.
퀵 정렬이 병합 정렬(Merge Sort)보다 실제로 선호되는 이유는 두 가지다.
병합 정렬은 분할된 배열을 병합할 때 임시 배열이 필요하다. 반면 퀵 정렬은 배열 내에서 Swap만으로 정렬하기 때문에 추가 메모리가 O(log N)(재귀 스택)만 필요하다.
퀵 정렬은 배열의 인접한 영역을 집중적으로 처리한다. Partition 과정에서 연속된 메모리를 읽고 쓰기 때문에 CPU 캐시 히트율이 높다. 반면 병합 정렬은 임시 배열에 복사하는 과정에서 캐시 미스가 많다.
현대 CPU는 캐시 성능에 크게 의존하기 때문에, 이론적 시간 복잡도가 같더라도 실제 실행 속도는 퀵 정렬이 훨씬 빠른 경우가 많다.
C++ std::sort는 순수한 퀵 정렬을 쓰지 않는다. Introsort라는 하이브리드 알고리즘을 쓴다.
Introsort 전략:
이렇게 하면 최악의 경우에도 O(N log N)을 보장하면서, 평균적으로는 퀵 정렬의 속도를 유지한다.
JavaScript의 V8 엔진은 TimSort(삽입 정렬 + 병합 정렬 하이브리드)를 쓰지만, 작은 배열에선 삽입 정렬을 쓰고, 큰 배열에선 퀵 정렬 기반 알고리즘을 혼용하는 경우도 있다.
퀵 정렬은 재귀 호출을 두 번 한다(왼쪽 부분, 오른쪽 부분). 이 때 스택 깊이가 O(log N)이 되도록 최적화할 수 있다.
방법: 큰 쪽 부분 배열을 반복문으로 처리하고, 작은 쪽만 재귀로 처리한다.
function quickSortOptimized(arr, low, high) {
while (low < high) {
const pi = partition(arr, low, high);
// 작은 쪽을 재귀로 처리
if (pi - low < high - pi) {
quickSortOptimized(arr, low, pi - 1);
low = pi + 1; // 큰 쪽은 반복문으로
} else {
quickSortOptimized(arr, pi + 1, high);
high = pi - 1; // 큰 쪽은 반복문으로
}
}
}
이렇게 하면 재귀 스택 깊이가 O(log N)으로 제한되어, 큰 배열에서도 스택 오버플로우 위험이 줄어든다.
아래는 Lomuto Partition + Median-of-Three Pivot을 쓰는 퀵 정렬 전체 구현이다.
function swap(arr, i, j) {
[arr[i], arr[j]] = [arr[j], arr[i]];
}
function medianOfThree(arr, low, high) {
const mid = Math.floor((low + high) / 2);
if (arr[low] > arr[mid]) swap(arr, low, mid);
if (arr[low] > arr[high]) swap(arr, low, high);
if (arr[mid] > arr[high]) swap(arr, mid, high);
swap(arr, mid, high); // 중간값을 끝으로
}
function partition(arr, low, high) {
medianOfThree(arr, low, high);
const pivot = arr[high];
let i = low - 1;
for (let j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return i + 1;
}
function quickSort(arr, low = 0, high = arr.length - 1) {
if (low < high) {
const pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
return arr;
}
// 테스트
const arr = [7, 2, 9, 1, 5, 3];
console.log('Before:', arr);
quickSort(arr);
console.log('After:', arr); // [1, 2, 3, 5, 7, 9]
초기 배열: [7, 2, 9, 1, 5, 3]
Step 1: Median-of-Three (low=0, mid=2, high=5)
Step 2: Partition around 7
[2, 1, 5, 3, 7, 9] (pi=4)Step 3: 왼쪽 재귀 [2, 1, 5, 3]
[1, 2, 5, 3] (pi=1)[1] (정렬 완료)[5, 3]Step 4: [5, 3] 재귀
[3, 5]Step 5: 오른쪽 재귀 [9]
최종 결과: [1, 2, 3, 5, 7, 9]
퀵 정렬을 공부하면서 깨달은 건, 알고리즘은 이론만으론 부족하다는 것이다. 평균 O(N log N), 최악 O(N²)이라는 수식만 외워서는 왜 실제로 퀵 정렬이 표준인지 이해할 수 없다.
직접 구현해보고, Partition 과정을 손으로 추적해보고, Pivot 선택 전략을 바꿔가며 실험해보니 비로소 감이 왔다. Cache Locality, In-Place Sorting, Tail-Call Optimization 같은 개념들이 단순한 용어가 아니라 실제 성능을 좌우하는 핵심 요소라는 걸 체감했다.
그리고 Introsort처럼 실제 라이브러리들이 순수한 퀵 정렬을 쓰지 않고 상황에 맞게 알고리즘을 혼합한다는 점도 흥미로웠다. 최악의 경우를 방지하려고 Heap Sort로 전환하고, 작은 배열에선 Insertion Sort를 쓰는 것처럼, 알고리즘도 현실과 타협한다.
퀵 정렬은 "빠르다"는 이름에 걸맞게, 평균적으로 가장 빠른 정렬이다. 하지만 그 "빠름"은 단순히 시간 복잡도만으로 설명되지 않는다. 메모리 효율, 캐시 활용, Pivot 전략, 하이브리드 최적화까지 모두 합쳐진 결과다.
이제 Array.sort()를 쓸 때마다, 그 뒤에서 Pivot을 고르고 배열을 나누는 퀵 정렬의 모습이 떠오른다. 그리고 그 과정이 왜 빠른지, 어떻게 최적화되는지 조금은 알 것 같다.